RADICACIÓN
En matemática, la potencia de un número es el
producto de factores iguales:
Esta
operación de elevar a una
potencia se llama involución ) . Al igual
que la adición y la multiplicación, la potenciación tiene una operación
inversa, pero operación unaria, llamada extracción de una raíz o
radicación (evolución).
Para cualquier entero positivo n, un número b es
la raíz enésima de a, si b es tal que,
donde n se
llama índice de la raíz, que indica qué raíz se va a hallar; a se
denomina radicando,
y b es la raíz enésima, por lo que se suele conocer también con ese nombre. La
expresión
se
llama radical. La notación a seguir tiene varias formas:
, la que
se prueba, igualando el radical a p; y la potencia 1/n a q, luego por
definición y propiedades de potencia resulta p = q.
Para todo n natural, a y b reales
positivos, se tiene la equivalencia:
.
Dentro de los números reales R+ positivos,
siempre puede encontrarse una única raíz enésima también positiva. Si el número a es
negativo entonces sólo existirá una raíz real cuando el índice n sea
impar3 . La raíz
enésima de un número negativo no es un número real (no está definida dentro de
los números reales) cuando el índice n es par.
Dentro de los números complejos C , para
cada número z siempre es posible encontrar exactamente n raíces
enésimas diferentes.
La raíz de orden dos se llama raíz cuadrada y, por ser
la más frecuente, se escribe sin superíndice: 
en vez
de
La raíz
de orden tres se llama raíz cúbica.
El cálculo efectivo de la raíz se hace mediante las funciones logaritmo y exponencial:
.
Este método es empleado comúnmente en calculadoras de bolsillo y
otro tipo de hardware.
El problema es
que dicho cálculo no funciona con los números negativos, porque el logaritmo
usual sólo está definido en (0,+ ∞). De ahí una tendencia, todavía minoritaria,
de restringir la definición de las raíces de orden impar
a
los números positivos.
Propiedades
Como se indica con la igualdad de la raíz,
la radicación es en realidad otra forma de expresar una potenciación:
la raíz de cierto orden de un número es equivalente a elevar dicho número a una
potencia, cuyo exponente es el inverso multiplicativo del índice . Por esto,
las propiedades de la
potenciación se cumplen también con la radicación. Para que estas propiedades
se cumplan, se exige que el radicando de las raíces sea positivo.
Ecuación Básica
Dada la ecuación
siendo a, b n reales positivos; caben
los tres casos:
1. Conocidos
a y n, se halla b mediante potenciación.
2. Conocidos
b y n, se halla a mediante radicación para n entero positivo, o bien elevando a
b a la potencia 1/n y hasta con radicales.
3. Dada,
llamada función
exponencial, no hay método general para despejar x por propiedades de la
potenciación. Se resuelve con logaritmos. De modo que
Raíz De Un Producto
La raíz de un producto es igual al producto
de las raíces de los factores nombrados anteriormente.
Ejemplo
=
=
Se llega a igual resultado de la siguiente
manera:
Raíz De Un Cociente
La raíz de una fracción es igual al cociente
de la raíz del numerador entre la raíz del denominador.
=
Ejemplo
=
Cuando esta propiedad se aplica a números, no
hace falta pasar la raíz a potencia de exponente racional, aunque sí cuando se
hace con variables.
Ejemplos
=
Raíz De Una Raíz
Para calcular la raíz de una raíz se multiplican
los índices de las raíces y se conserva el radicando.
=
Ejemplo
=
Potencia De Una Raíz
Para calcular la potencia de una raíz se
eleva el radicando a esa potencia.
Ejemplo
=
Otras Propiedades
Utilizando las propiedades fundamentales, se
pueden obtener otras propiedades interesantes, como por ejemplo, el cálculo de
la raíz de un producto con el mismo radicando y distintos índices, que se
obtiene multiplicando los índices de las raíces y conservando el radicando
elevado a la suma de los índices.
No nos podemos olvidar de la propiedad radicando
negativo, en donde el índice se convierte en denominador y el 1 en numerador.
Números Complejos
Si z es un número complejo, entonces admite una representación mediante módulo y argumento (forma polar) de
la forma:
,
donde 
De esta manera, en forma polar, las raíces n-ésimas de z, necesarias para la ecuación,
pueden ser calculadas por medio de la
fórmula
Por tanto, un número complejo tiene n raíces enésimas distintas. En el plano complejo están dispuestas en los vértices de un polígono regular de n lados con centro en el origen del plano
complejo. La raíz cúbica y la distancia del centro de dicho polígono a sus
vértices son
Ejemplo
EJERCICIOS DESARROLLADOS RADICACION
1. Calcula los
valores de las siguientes potencias:
2. Extraer
factores del radical:
3. Introducir
factores:
4. Realiza las
sumas de radicales:
EJERCICIOS PARA RESOLVER
RADICACION
1.
Halla las sumas:
2.
Efectúa las sumas:
3.
Realizar los productos:
4.
Efectúa las divisiones de radicales:
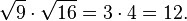
No hay comentarios:
Publicar un comentario