INECUACIONES
Del mismo modo en que se hace la diferencia de igualdad y ecuación, una
inecuación que es válida para todas las variables se llama inecuación incondicional y las
que son válidas solo para algunos valores de las variables se conocen
como inecuaciones condicionales.
Los valores que verifican la desigualdad, son sus soluciones.
·
Ejemplo de inecuación incondicional: .
·
Ejemplo de inecuación condicional: .
Clasificación
Los criterios más comunes de clasificación
del ejemplo:
·
De dos incógnitas. Ejemplo:
·
De tres incógnitas. Ejemplo:
Según
la potencia de la incógnita,
·
De primer grado o lineal. Cuando el
mayor exponente de la incógnita de la inecuación es uno. Ejemplo:
·
De segundo grado o cuadrática. Cuando
el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo:
·
De tercer grado o cúbica. Cuando el
mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo:
Nota: estas clasificaciones no son mutuamente
excluyentes, como se muestra en el último ejemplo.
Inecuaciones
De Segundo Grado Con Una Incógnita
Se expresan a través de cualquiera de las
desigualdades siguientes (con a, b y c números reales, y a distinto de cero):
Sistema De
Inecuaciones
La región
de viabilidad en un problema de programación
lineal está
definida por un sistema de inecuaciones.
En un sistema de
inecuaciones intervienen dos o más inecuaciones. No todos
los sistemas de inecuaciones tienen solución.
Sistema De Inecuaciones De Primer Grado
Con Una Incógnita
Es un conjunto de inecuaciones de primer
grado con la misma variable:
La solución del sistema será el conjunto de números
reales que verifican a la vez todas las inecuaciones.
EJERCICIOS DESARROLLADOS INECUACIONES
1.
Resolver las siguientes
inecuaciones
(1, ∞)
2.
Resuelve el sistema:
(x +1) · 10 + x ≤ 6 (2x + 1)
10x + 10 + x ≤ 12 x + 6
10 x + x - 12x ≤ 6 - 10
−x ≤ − 4 x ≥ 4
[4, 7)
3.
Resolver las inecuaciones:
·
7x2 + 21x − 28 < 0
x2 +3x − 4 < 0
x2 +3x − 4 = 0
P(−6) = (−6)2 +3 · (−6)− 4 > 0
P(0) = 02 +3 · 0 − 4 < 0
P(3) = 32 +3 · 3 − 4 > 0
(−4, 1)
·
−x2 + 4x − 7 < 0
x2 − 4x + 7 = 0
P(0) = −02 + 4 ·0 − 7 < 0
S =
P(−3) = 4 ·
(−3)2 − 16 > 0
P(0) = 4 · 0 2 − 16 < 0
P(3) = 4 · 3 2 − 16 > 0
(-∞ , −2 ]  [2, +∞)
[2, +∞)
EJERCICIOS PARA RESOLVER
INECUACIONES
1.
Resuelve:
·
x4 − 25x2 + 144 < 0
·
x4 − 16x2 − 225 ≥ 0
2.
Resolver las inecuaciones:





























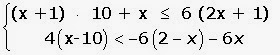










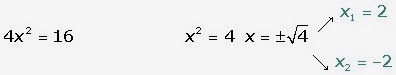





No hay comentarios:
Publicar un comentario